bidirectional transmittance distribution function (BTDF)

[7.5.3.16] f_t^*

The ratio of the differential luminance dL_t(θ_t, ϕ_t) for a ray transmitted in a given direction(θ_t, ϕ_t) to the differential luminous flux density dE_i(θ_i, ϕ_i), incident from a given direction (θ_i, ϕ_i), that produces it (see Figure 23).
Units = sr^-1

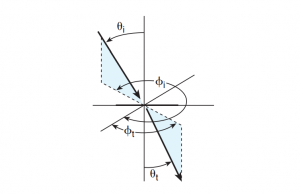
f_{t}\left (\theta _{i},\phi _{i}; \theta _{t},\phi _{t} \right )]\equiv \frac{dL_{t}\left ( \theta _{t},\phi _{t} \right )}{dE_{i}\left ( \theta _{i},\phi _{i} \right)} = \frac{dL_{t}\left ( \theta _{t},\phi _{t} \right )}{L_{i}\left ( \theta _{i},\phi _{i} \right )d\Omega _{i}} ,

where dΩ ≡ dω · cos θ

Notes:

(i) This distribution function is the basic parameter for describing (geometrically) the transmitting properties of a thin scattering film (with negligible internal scattering) so that the transmitted radiation emerges from a point that is not significantly separated from the point of incidence of the incident ray(s). The governing considerations are similar to those for application of the bidirectional reflectance-distribution function (BRDF), rather than the bidirectional scattering-surface reflectance-distribution function (BSSRDF), as discussed in Nicodemus.*

(ii) It may have any positive value and will approach infinity in the direction for regular transmission (possibly refraction but without scattering).

(iii) The spectral and polarization aspects must be defined for complete specification, since the BTDF as given above only defines the geometrical aspects.

^{* Nicodemus FE. et al, Geometrical Considerations and Nomenclature for Reflectance, NBS Monograph 160. Washington DC: U.S. Department of Commerce; Oct 1977.}