[7.3.3.17] fr*
The ratio of the differential luminance of a ray dLr(θr,φr) reflected in a given direction (θr,φr) to the differential luminous flux density dEi(θi,φi) incident from a given direction (θi,φi) that produces it.
Units: sr-1
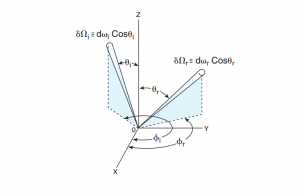
f_{r}\left (\theta _{i},\phi _{i}; \theta _{r},\phi _{r} \right ) \equiv \frac{dL_{r}\left ( \theta _{r},\phi _{r} \right )}{dE_{i}\left ( \theta _{i},\phi _{i} \right )} = \frac{dL_{r}\left ( \theta _{r},\phi _{r} \right )}{L_{i}\left ( \theta _{i},\phi _{i} \right )d\Omega _{i}} ,
where dΩ ≡ dω · cos θ
Notes:
(i) This distribution function is the basic parameter for describing (geometrically) the reflecting properties of an opaque surface element (negligible internal scattering).
(ii) It may have any positive value and will approach infinity in the specular direction for ideally specular reflectors.
(iii) The spectral and polarization aspects must be defined for complete specification, since the BRDF as given above only defines the geometric aspects.
* Nicodemus FE, et al. Geometrical Considerations and Nomenclature for Reflectance, NBS Monograph 160. Washington, DC: U.S. Department of Commerce; Oct 1977.
« Back to Definitions Index