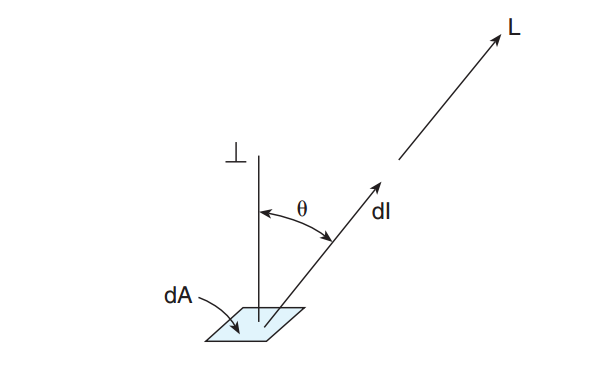
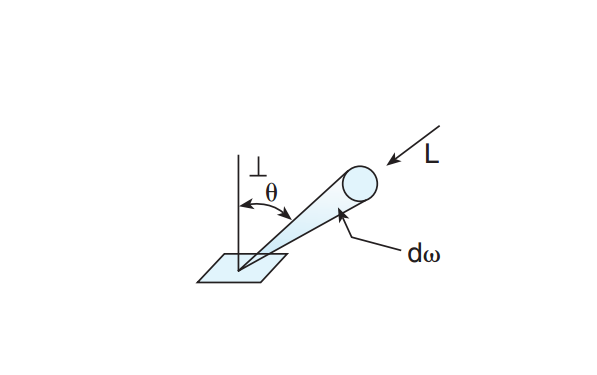
[3.5] L = d2 Φ | (d ωdA cos Θ)
(in a direction and at a point on a real or imaginary surface)
The quotient of the luminous flux at an element of the surface surrounding the point, and propagated in directions defined by an elementary cone containing the given direction, by the product of the solid angle of the cone and the area of the orthogonal projection of the element of the surface on a plane perpendicular to the given direction. The luminous flux may be leaving, passing through, and/or arriving at the surface. Formerly, photometric brightness. (See Figure 1.)
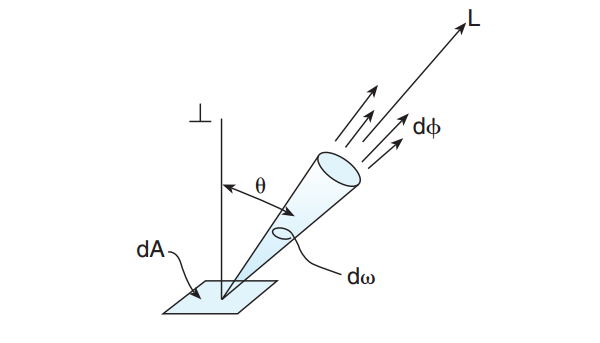
By introducing the concept of luminous intensity, luminance may be expressed as (see Figure 2):
Luminance may be measured at a receiving surface by using:
Note: In common usage, the term brightness usually refers to the strength of sensation that results from viewing surfaces or spaces from which light comes to the eye. This sensation is determined in part by the definitely measurable luminance defined above and in part by conditions of observation, such as the state of adaptation of the eye. (See brightness.)
In much of the literature, the term brightness, used alone, refers to both luminance and sensation. The context usually indicates which meaning is intended. Previous usage notwithstanding, neither the term brightness, nor the term photometric brightness should be used to denote the concept of luminance.